Snub 24-cell honeycomb

Snub 24-cell honeycomb
(No image)
Type Uniform honeycomb
Schläfli symbols h0,1{3,4,3,3}
h0,1,2{3,3,4,3}
h1,2,3{4,3,3,4}
h1,2,3{4,3,31,1}
s{31,1,1,1}
Coxeter-Dynkin diagrams




4-face type snub 24-cell
16-cell
5-cell
Cell type {3,3}
{3,5}
Face type triangle {3}
Vertex figure
Irregular decachoron
Coxeter groups 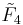{\tilde{F}}_4, [3,4,3,3] (half)
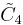{\tilde{C}}_4, [4,3,3,4] (half)
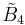{\tilde{B}}_4, [4,3,31,1] (half)
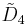{\tilde{D}}_4, [31,1,1,1] (half)
Symmetry groups [3+,4,3,3]
[3,4,(3,3)+]
[4,(3,3)+,4]
[4,(3,31,1)+]
[31,1,1,1]+
Properties Vertex transitive, nonWythoffian

In four-dimensional Euclidean geometry, the snub 24-cell honeycomb, or snub icositetrachoric honeycomb is a uniform space-filling tessellation (or honeycomb) by snub 24-cells, 16-cells, and 5-cells. It was discovered by Thorold Gosset with his 1900 paper of semiregular polytopes. It is not semiregular by Gosset's definition of regular facets, but all of its cells (ridges) are regular, either tetrahedra or icosahedra.

It can be seen as an alternation of a truncated 24-cell honeycomb, and can be represented by Schläfli symbol h0,1{3,4,3,3}.

It is defined by an irregular decachoron vertex figure (10-celled 4-polytope), faceted by four snub 24-cells, one 16-cell, and five 5-cells. The vertex figure can be seen topologically as a modified tetrahedral prism, where one of the tetrahedra is subdivided at mid-edges into a central octahedron and four corner tetrahedra. Then the four side-facets of the prism, the triangular prisms become tridiminished icosahedra.

Symmetry constructions

There are five different symmetry constructions of this tessellation. Each symmetry can be represented by different arrangements of colored snub 24-cell, 16-cell, and 5-cell facets. In all cases, four snub 24-cells, five 5-cells, and one 16-cell meet at each vertex, but the vertex figures have different symmetry generators.

Coxeter group Full symmetry
group
Coxeter notation		 Coxeter-Dynkin diagram Facets (on vertex figure)
Snub 24-cell
(4)		 16-cell
(1)		 5-cell
(5)
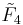{\tilde{F}}_4 = [3,4,3,3] [3+,4,3,3] 4:
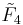{\tilde{F}}_4 = [3,4,3,3] [3,4,(3,3)+] 3:
1:
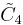{\tilde{C}}_4 = [4,3,3,4] [[4,(3,3)+,4]] 2,2:
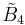{\tilde{B}}_4 = [31,1,3,4] <[(31,1,3)+,4]> = [4,(3,3)+,4] 1,1:
2:
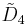{\tilde{D}}_4 = [31,1,1,1] [3,3[31,1,1,1]+] = [3+,3,4,3] 1,1,1,1:

See also

References